RGBQCD

I'm still thinking how sense of magnitude gets confounded when we look at certain shapes. Look, for example, at these pictures of mountains and how it’s difficult to tell how big the mountain is when you only have the surrounding rocks to compare to. The effect is shown more starkly in a previous post which showed Base Camp of Everest.

This is a classical example of a property called self-similarity. As you zoom in or zoom out, the complexity of the rock’s shape seems to be preserved- the shape of craggy cliff is copied again at different orders of magnitude.

I was talking to a friend of mine about this a few weeks ago, and he pointed another example of another convergence at two different orders of magnitude- this picture of dried mud compared with the zoomed in pictured of dried blood.

What’s interesting here is that in the blood and the mud, the cracked surfaces look almost indistinguishable. My friend pointed out that both would have begun as viscous liquids and the physics of their drying probably overlap and follow the same differential equations. This comment made me think about the concept of the attractor, and how the look of the cracked surface (that also looks like a birds-eye-view of a ravine) may fulfill the definition of being an attractor of both drying blood and mud.

So let’s talk about attractors. They are properties of a system that compel it to move in a certain direction, no matter what the starting conditions of the system are. A kinda-cool-but-not-really-cool example of an attractor is the point at the bottom of a damped pendulum system where the pendulum eventually stops after all its energy is dissipated. An actually-really-cool example of an attractor is the Sierpinski Gasket, a fractal that is wholly described by something called an Iterated Function System (or IFS). An IFS, basically, is a set of instructions that tell you how to manipulate an image over and over and over again, for an infinite number of times. Let me give an example. Let’s start with a cat as our initial condition (can you tell I drew it myself?):

Now, my IFS is a set of instructions that says something like, “Take your cat, make three copies, shrink the copies down to a quarter of the original size, and arrange the copies in the shape of a right triangle” Like so:

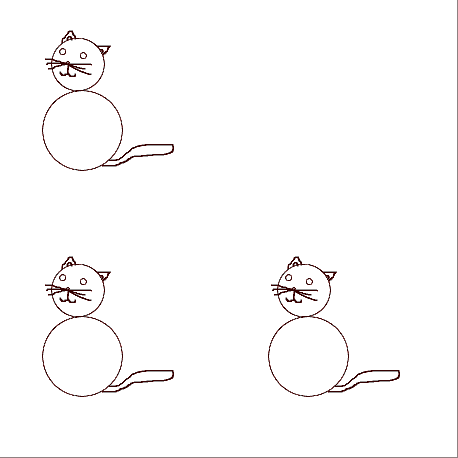
Now the IFS says to do the same set of operations again-

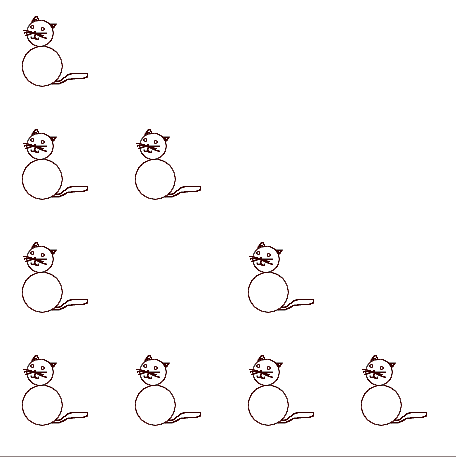
and again

and again

onto infinity

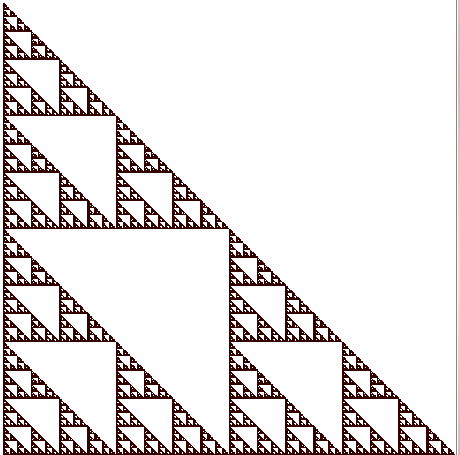
The shape we get at the end is this very interesting fractal shape called the Sierpinski Gasket. The fascinating thing is that there really is no trace of the underlying cat we started with at all. Really, we could begin with any starting image, whether it be a cat, or a house, or a pile of dirt, and by applying the IFS to it, we would end up again at the Sierpinski Gasket. Like an incredible infatuation, we can’t help end up at the Gasket, no matter how dissimilar our base image is from the final fractal. That’s why the fractal is the attractor of the IFS!

The Gasket also exhibits striking self-similarity. Zoom in on any part of the Gasket, and the entire gasket will appear again in the tiny part. You could never actually tell how deep you were in the fractal, because each level looks the same as the zoomed in or zoomed out picture. Order of magnitude is practically impossible to tell in a fractal.

It’s interesting to think about the fractal nature of Nature. We know that self-similarity is a large part of what makes the size of mountains difficult to judge. It also seems that no matter whether you begin with blood or mud, whether it’s at the scale of a field or on a microscope slide, their drying properties will attract them to the shape of a cracked, dendritic web.